What Is The Angle From Vertical Of The Axis Of The Second Polarizing Filter?

The Nature of Lite

8 Polarization

Learning Objectives

Past the finish of this section, you will be able to:

Explain the change in intensity as polarized light passes through a polarizing filter
Calculate the effect of polarization past reflection and Brewster'due south bending
Describe the effect of polarization past handful
Explicate the use of polarizing materials in devices such as LCDs

Polarizing sunglasses are familiar to about of u.s.a.. They take a special ability to cut the glare of light reflected from h2o or glass ((Figure)). They accept this ability because of a wave characteristic of low-cal called polarization. What is polarization? How is it produced? What are some of its uses? The answers to these questions are related to the wave character of lite.

These 2 photographs of a river show the effect of a polarizing filter in reducing glare in light reflected from the surface of h2o. Part (b) of this figure was taken with a polarizing filter and part (a) was not. Equally a result, the reflection of clouds and sky observed in part (a) is not observed in office (b). Polarizing sunglasses are particularly useful on snowfall and water. (credit a and credit b: modifications of work by "Amithshs"/Wikimedia Commons)

The figure has two photographs of the same part of a river. In figure a, the clouds and sky are reflected in the water, making it hard to see the stones at the bottom of the river. In figure b, the reflection of the sky is absent and the bottom of the river can be seen more clearly.

Malus'due south Law

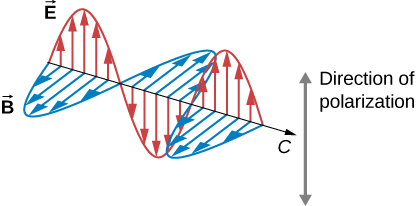
Light is one type of electromagnetic (EM) wave. Every bit noted in the previous chapter on Electromagnetic Waves, EM waves are transverse waves consisting of varying electric and magnetic fields that oscillate perpendicular to the direction of propagation ((Figure)). Withal, in general, in that location are no specific directions for the oscillations of the electric and magnetic fields; they vibrate in any randomly oriented plane perpendicular to the direction of propagation. Polarization is the attribute that a wave's oscillations practise have a definite management relative to the direction of propagation of the moving ridge. (This is not the same blazon of polarization every bit that discussed for the separation of charges.) Waves having such a management are said to be polarized. For an EM wave, we define the direction of polarization to exist the direction parallel to the electric field. Thus, we can think of the electrical field arrows as showing the direction of polarization, as in (Figure).

An EM wave, such as lite, is a transverse wave. The electric $\left(\stackrel{\to }{E}\right)$ and magnetic $\left(\stackrel{\to }{B}\right)$ fields are perpendicular to the direction of propagation. The direction of polarization of the wave is the direction of the electrical field.

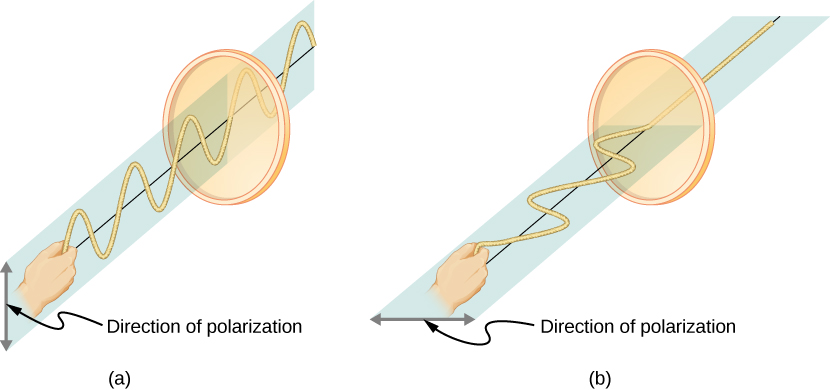
To examine this further, consider the transverse waves in the ropes shown in (Effigy). The oscillations in ane rope are in a vertical airplane and are said to be vertically polarized. Those in the other rope are in a horizontal aeroplane and are horizontally polarized. If a vertical slit is placed on the first rope, the waves pass through. However, a vertical slit blocks the horizontally polarized waves. For EM waves, the direction of the electric field is coordinating to the disturbances on the ropes.

The transverse oscillations in one rope (a) are in a vertical airplane, and those in the other rope (b) are in a horizontal plane. The commencement is said to be vertically polarized, and the other is said to be horizontally polarized. Vertical slits pass vertically polarized waves and block horizontally polarized waves.

Figure a shows waves on a vertically oscillating rope that pass through a vertical slit. The vertical oscillation is the direction of polarization. Figure b shows waves on a horizontally oscillating rope that do not pass through a similar vertical slit. The horizontal oscillation is the direction of polarization.

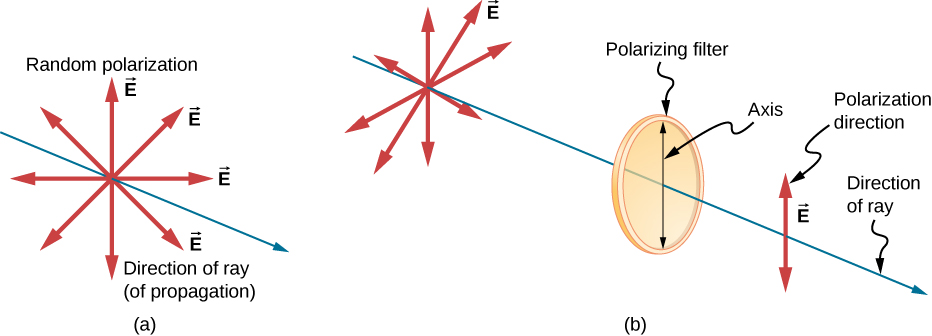
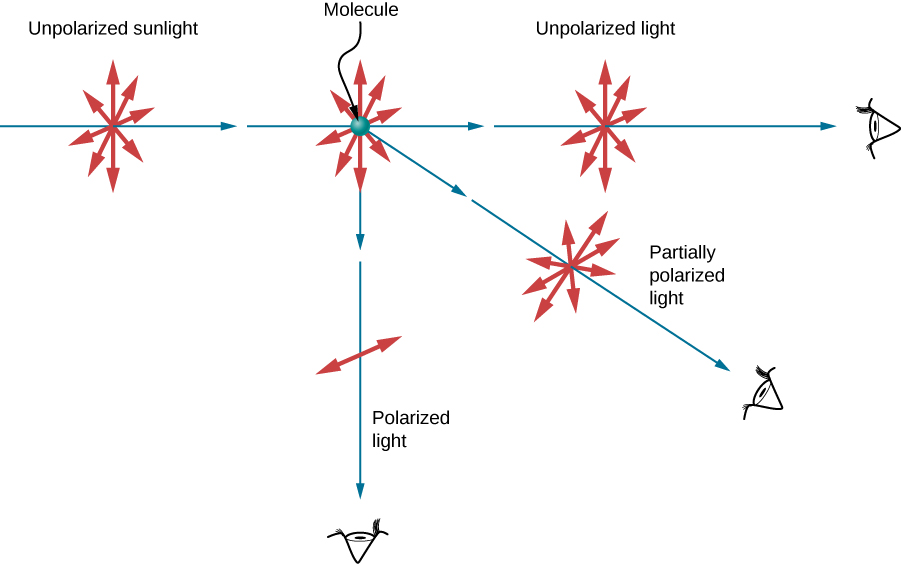
The Dominicus and many other light sources produce waves that have the electric fields in random directions ((Effigy)(a)). Such light is said to be unpolarized, considering it is composed of many waves with all possible directions of polarization. Polaroid materials—which were invented by the founder of the Polaroid Corporation, Edwin Land—act as a polarizing slit for lite, assuasive simply polarization in ane management to pass through. Polarizing filters are equanimous of long molecules aligned in one direction. If we think of the molecules every bit many slits, analogous to those for the oscillating ropes, nosotros can empathize why only calorie-free with a specific polarization tin go through. The axis of a polarizing filter is the direction along which the filter passes the electrical field of an EM moving ridge.

The slender pointer represents a ray of unpolarized light. The bold arrows represent the direction of polarization of the individual waves composing the ray. (a) If the light is unpolarized, the arrows point in all directions. (b) A polarizing filter has a polarization axis that acts as a slit passing through electric fields parallel to its direction. The direction of polarization of an EM wave is defined to exist the direction of its electric field.

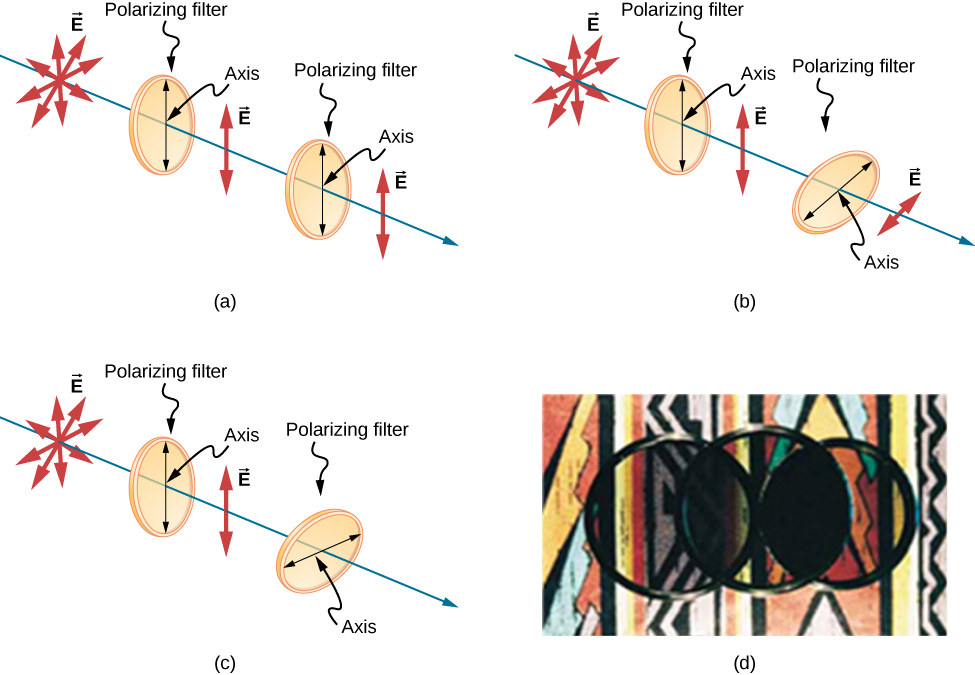
(Figure) shows the effect of 2 polarizing filters on originally unpolarized low-cal. The get-go filter polarizes the light along its axis. When the axes of the first and 2d filters are aligned (parallel), then all of the polarized light passed by the get-go filter is also passed by the second filter. If the second polarizing filter is rotated, only the component of the calorie-free parallel to the second filter's centrality is passed. When the axes are perpendicular, no light is passed by the 2nd filter.

The event of rotating 2 polarizing filters, where the first polarizes the light. (a) All of the polarized light is passed by the second polarizing filter, because its axis is parallel to the first. (b) Equally the 2nd filter is rotated, simply part of the light is passed. (c) When the 2nd filter is perpendicular to the first, no low-cal is passed. (d) In this photograph, a polarizing filter is placed in a higher place two others. Its axis is perpendicular to the filter on the right (night surface area) and parallel to the filter on the left (lighter area). (credit d: modification of piece of work by P.P. Urone)

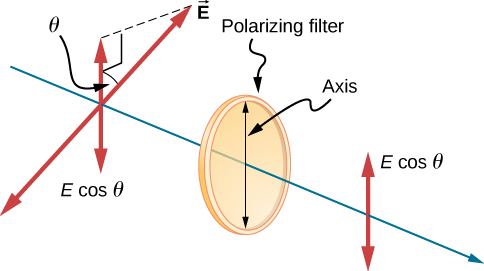
Just the component of the EM wave parallel to the centrality of a filter is passed. Allow u.s. call the bending between the direction of polarization and the axis of a filter $\theta$ . If the electric field has an aamplitude E, so the transmitted office of the moving ridge has an amplitude $E\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\theta$ ((Figure)). Since the intensity of a wave is proportional to its aamplitude squared, the intensity I of the transmitted wave is related to the incident wave by

$I={I}_{0}\phantom{\rule{0.2em}{0ex}}{\text{cos}}^{2}\phantom{\rule{0.2em}{0ex}}\theta$

where ${I}_{0}$ is the intensity of the polarized wave earlier passing through the filter. This equation is known as Malus's constabulary.

A polarizing filter transmits merely the component of the wave parallel to its axis, reducing the intensity of any low-cal not polarized parallel to its axis.

This Open Source Physics animation helps yous visualize the electric field vectors as light encounters a polarizing filter. Y'all can rotate the filter—note that the angle displayed is in radians. You can also rotate the animation for 3D visualization.

Check Your Understanding Although we did not specify the direction in (Figure), let's say the polarizing filter was rotated clockwise past $71.6\text{°}$ to reduce the light intensity past $90.0\text{%}$ . What would be the intensity reduction if the polarizing filter were rotated counterclockwise past $71.6\text{°}$ ?

also $90.0\text{%}$

Polarization by Reflection

By now, you tin probably estimate that polarizing sunglasses cut the glare in reflected light, because that light is polarized. You lot can check this for yourself by holding polarizing sunglasses in forepart of you and rotating them while looking at low-cal reflected from water or glass. As yous rotate the sunglasses, you will notice the light gets bright and dim, but not completely black. This implies the reflected light is partially polarized and cannot be completely blocked by a polarizing filter.

(Figure) illustrates what happens when unpolarized lite is reflected from a surface. Vertically polarized light is preferentially refracted at the surface, so the reflected low-cal is left more horizontally polarized. The reasons for this phenomenon are beyond the scope of this text, only a convenient mnemonic for remembering this is to imagine the polarization direction to be like an arrow. Vertical polarization is like an arrow perpendicular to the surface and is more than likely to stick and not exist reflected. Horizontal polarization is like an arrow bouncing on its side and is more than probable to exist reflected. Sunglasses with vertical axes thus cake more than reflected light than unpolarized light from other sources.

Polarization by reflection. Unpolarized calorie-free has equal amounts of vertical and horizontal polarization. After interaction with a surface, the vertical components are preferentially absorbed or refracted, leaving the reflected light more than horizontally polarized. This is akin to arrows striking on their sides and billowy off, whereas arrows hit on their tips go into the surface.

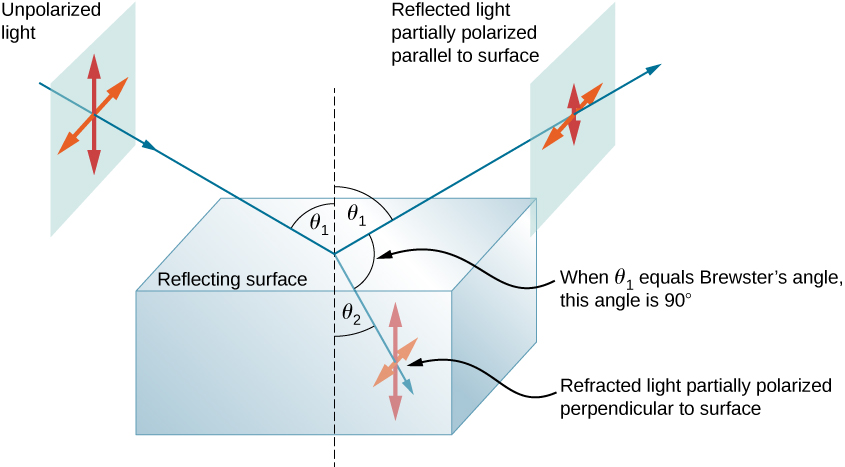
$The figure is a diagram that shows a block of glass in air. The reflecting surface is horizontal. A ray labeled unpolarized light starts at the upper left and hits the center of the block, at an angle theta one to the vertical. Centered on this incident ray is are two double headed arrows, one horizontal and the other vertical. From the point where this ray hits the glass block, two rays emerge. One is the reflected ray that goes up and to the right at an angle of theta one to the vertical, and the second is a refracted ray that goes down and to the right at an angle of theta two to the vertical. The reflected light is labeled as partially polarized parallel to the surface. Two double headed arrows, similar to those on the incident ray, are shown centered on the reflected ray, but the vertical arrow is significantly shorter than the horizontal one. The refracted ray is labeled as partially polarized perpendicular to the surface. Two double headed arrows, similar to those on the incident ray, are shown centered on the reflected ray, but the horizontal arrow is significantly shorter than the vertical one. A note indicates that when theta one equals Brewster's angle, the angle between the reflected and refracted ray is ninety degrees.$

Since the part of the calorie-free that is not reflected is refracted, the corporeality of polarization depends on the indices of refraction of the media involved. It tin can be shown that reflected light is completely polarized at an angle of reflection ${\theta }_{\text{b}}$ given by

$\text{tan}\phantom{\rule{0.2em}{0ex}}{\theta }_{\text{b}}=\frac{{n}_{2}}{{n}_{1}}$

where ${n}_{1}$ is the medium in which the incident and reflected calorie-free travel and ${n}_{2}$ is the index of refraction of the medium that forms the interface that reflects the low-cal. This equation is known as Brewster's law and ${\theta }_{\text{b}}$ is known every bit Brewster'southward angle, named after the nineteenth-century Scottish physicist who discovered them.

This Open Source Physics animation shows incident, reflected, and refracted light every bit rays and EM waves. Try rotating the blitheness for 3D visualization and likewise modify the angle of incidence. Near Brewster'southward angle, the reflected light becomes highly polarized.

Calculating Polarization by Reflection (a) At what angle will calorie-free traveling in air be completely polarized horizontally when reflected from water? (b) From glass?

Strategy All nosotros need to solve these issues are the indices of refraction. Air has ${n}_{1}=1.00,$ water has ${n}_{2}=1.333,$ and crown glass has ${n}_{2}^{\text{′}}=1.520.$ The equation $\text{tan}\phantom{\rule{0.2em}{0ex}}{\theta }_{\text{b}}=\frac{{n}_{2}}{{n}_{1}}$ can exist directly applied to observe ${\theta }_{\text{b}}$ in each example.

Solution

Putting the known quantities into the equation

$\text{tan}\phantom{\rule{0.2em}{0ex}}{\theta }_{\text{b}}=\frac{{n}_{2}}{{n}_{1}}$

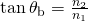
gives

$\text{tan}\phantom{\rule{0.2em}{0ex}}{\theta }_{\text{b}}=\frac{{n}_{2}}{{n}_{1}}=\frac{1.333}{1.00}=1.333.$

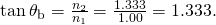
Solving for the angle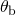 ${\theta }_{\text{b}}$ yields

${\theta }_{\text{b}}={\text{tan}}^{-1}\phantom{\rule{0.2em}{0ex}}1.333=53.1\text{°}.$
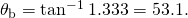
Similarly, for crown glass and air,

$\text{tan}\phantom{\rule{0.2em}{0ex}}{\theta }_{\text{b}}^{\text{′}}=\frac{{n}_{2}^{\text{′}}}{{n}_{1}}=\frac{1.520}{1.00}=1.52.$

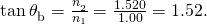
Thus,

${\theta }_{\text{b}}^{\text{′}}={\text{tan}}^{-1}\phantom{\rule{0.2em}{0ex}}1.52=56.7\text{°}.$

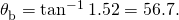
Significance Low-cal reflected at these angles could be completely blocked by a good polarizing filter held with its axis vertical. Brewster'due south angle for water and air are similar to those for glass and air, and so that sunglasses are equally effective for light reflected from either water or glass under similar circumstances. Light that is not reflected is refracted into these media. Therefore, at an incident bending equal to Brewster's angle, the refracted light is slightly polarized vertically. It is not completely polarized vertically, because only a pocket-sized fraction of the incident light is reflected, so a meaning amount of horizontally polarized light is refracted.

Check Your Understanding What happens at Brewster's angle if the original incident low-cal is already $100\text{%}$ vertically polarized?

In that location will be simply refraction just no reflection.

Atomic Explanation of Polarizing Filters

Polarizing filters have a polarization centrality that acts as a slit. This slit passes EM waves (often visible light) that accept an electrical field parallel to the axis. This is accomplished with long molecules aligned perpendicular to the axis, as shown in (Figure).

Long molecules are aligned perpendicular to the axis of a polarizing filter. In an EM wave, the component of the electrical field perpendicular to these molecules passes through the filter, whereas the component parallel to the molecules is captivated.

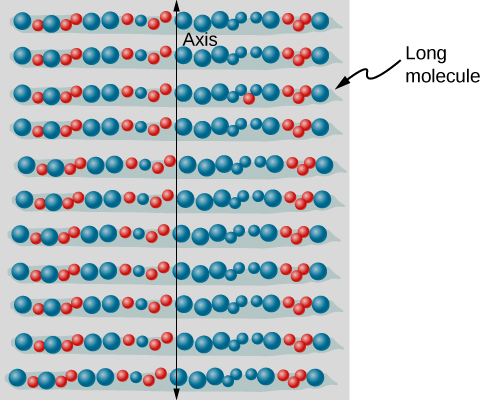
The figure shows an illustration of a stack of long identical horizontal molecules. A vertical axis is drawn over the molecules.

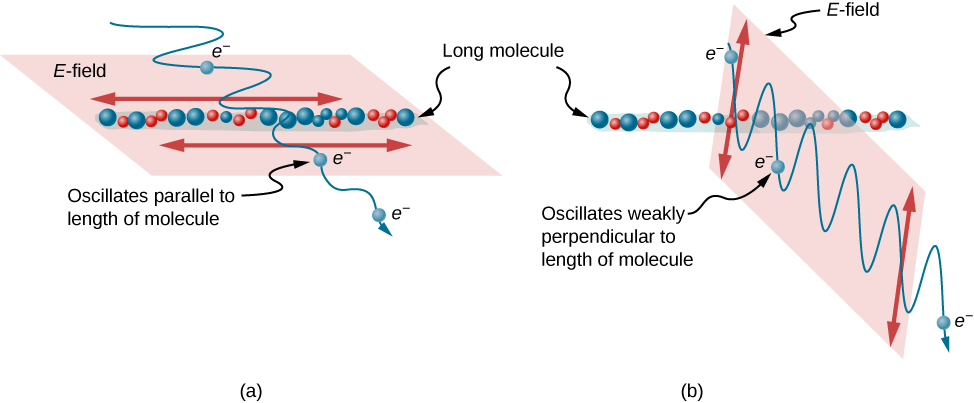
(Figure) illustrates how the component of the electric field parallel to the long molecules is captivated. An EM moving ridge is composed of aquiver electrical and magnetic fields. The electrical field is strong compared with the magnetic field and is more constructive in exerting force on charges in the molecules. The most afflicted charged particles are the electrons, since electron masses are small. If an electron is forced to oscillate, information technology can absorb energy from the EM wave. This reduces the field in the wave and, hence, reduces its intensity. In long molecules, electrons can more hands oscillate parallel to the molecule than in the perpendicular direction. The electrons are spring to the molecule and are more restricted in their movement perpendicular to the molecule. Thus, the electrons tin absorb EM waves that take a component of their electric field parallel to the molecule. The electrons are much less responsive to electrical fields perpendicular to the molecule and let these fields to pass. Thus, the centrality of the polarizing filter is perpendicular to the length of the molecule.

Diagram of an electron in a long molecule oscillating parallel to the molecule. The oscillation of the electron absorbs energy and reduces the intensity of the component of the EM wave that is parallel to the molecule.

Polarization by Handful

If y'all hold your polarizing sunglasses in front of you and rotate them while looking at blue sky, you will see the sky get bright and dim. This is a clear indication that light scattered by air is partially polarized. (Figure) helps illustrate how this happens. Since light is a transverse EM wave, it vibrates the electrons of air molecules perpendicular to the direction that information technology is traveling. The electrons then radiate like small antennae. Since they are oscillating perpendicular to the direction of the lite ray, they produce EM radiation that is polarized perpendicular to the direction of the ray. When viewing the light along a line perpendicular to the original ray, as in the effigy, at that place can be no polarization in the scattered light parallel to the original ray, considering that would require the original ray to exist a longitudinal wave. Forth other directions, a component of the other polarization can be projected along the line of sight, and the scattered light is simply partially polarized. Furthermore, multiple scattering can bring calorie-free to your eyes from other directions and can contain different polarizations.

Polarization past handful. Unpolarized calorie-free scattering from air molecules shakes their electrons perpendicular to the direction of the original ray. The scattered light therefore has a polarization perpendicular to the original direction and none parallel to the original direction.

Photographs of the sky can be darkened past polarizing filters, a pull a fast one on used by many photographers to make clouds brighter by contrast. Scattering from other particles, such equally smoke or dust, can also polarize lite. Detecting polarization in scattered EM waves can be a useful belittling tool in determining the handful source.

A range of optical effects are used in sunglasses. As well existence polarizing, sunglasses may have colored pigments embedded in them, whereas others use either a nonreflective or reflective coating. A recent development is photochromic lenses, which darken in the sunlight and become clear indoors. Photochromic lenses are embedded with organic microcrystalline molecules that alter their properties when exposed to UV in sunlight, but become articulate in bogus lighting with no UV.

Liquid Crystals and Other Polarization Effects in Materials

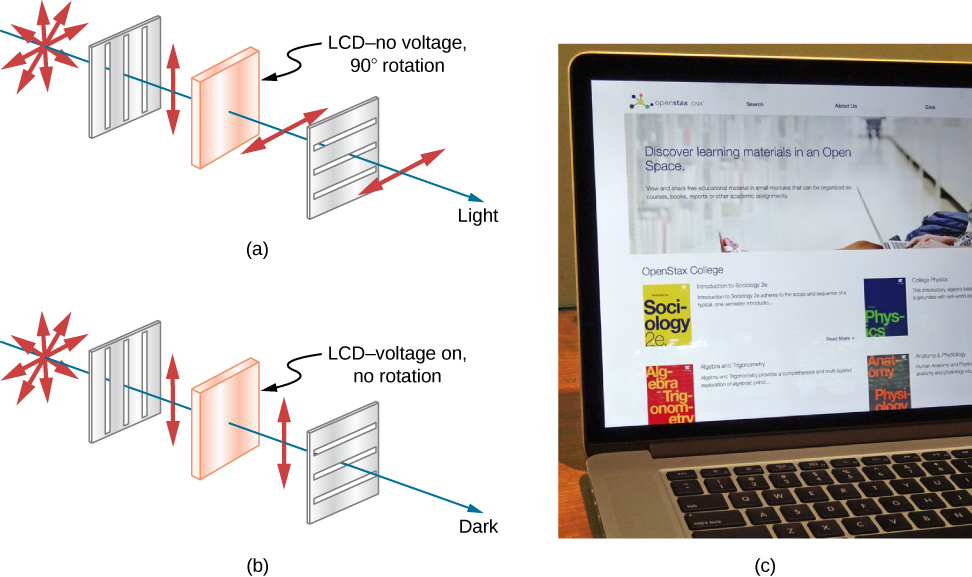
Although you are undoubtedly aware of liquid crystal displays (LCDs) found in watches, calculators, estimator screens, cellphones, apartment screen televisions, and many other places, y'all may non be enlightened that they are based on polarization. Liquid crystals are and so named considering their molecules can be aligned even though they are in a liquid. Liquid crystals have the property that they can rotate the polarization of calorie-free passing through them by $90\text{°}$ . Furthermore, this property tin can exist turned off by the application of a voltage, as illustrated in (Figure). It is possible to dispense this characteristic speedily and in pocket-size, well-defined regions to create the contrast patterns we run into in and then many LCD devices.

In apartment screen LCD televisions, a large light is generated at the back of the Telly. The light travels to the front end screen through millions of tiny units called pixels (pic elements). One of these is shown in (Figure)(a) and (b). Each unit has three cells, with red, blueish, or greenish filters, each controlled independently. When the voltage across a liquid crystal is switched off, the liquid crystal passes the low-cal through the detail filter. We can vary the flick dissimilarity by varying the strength of the voltage practical to the liquid crystal.

(a) Polarized calorie-free is rotated $90\text{°}$ by a liquid crystal and then passed by a polarizing filter that has its centrality perpendicular to the direction of the original polarization. (b) When a voltage is applied to the liquid crystal, the polarized light is non rotated and is blocked by the filter, making the region dark in comparison with its surroundings. (c) LCDs can be fabricated color specific, small, and fast enough to utilise in laptop computers and TVs. (credit c: modification of work past Jane Whitney)

Many crystals and solutions rotate the plane of polarization of light passing through them. Such substances are said to be optically agile. Examples include sugar water, insulin, and collagen ((Figure)). In addition to depending on the type of substance, the amount and direction of rotation depend on several other factors. Amongst these is the concentration of the substance, the altitude the lite travels through it, and the wavelength of light. Optical activity is due to the asymmetrical shape of molecules in the substance, such as being helical. Measurements of the rotation of polarized light passing through substances can thus be used to measure concentrations, a standard technique for sugars. It tin also requite data on the shapes of molecules, such as proteins, and factors that bear on their shapes, such as temperature and pH.

Optical activeness is the ability of some substances to rotate the plane of polarization of light passing through them. The rotation is detected with a polarizing filter or analyzer.

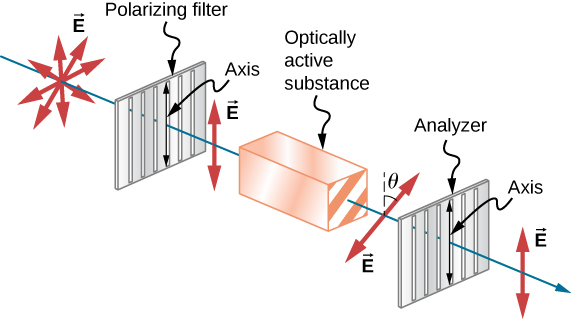
Glass and plastic become optically agile when stressed: the greater the stress, the greater the effect. Optical stress analysis on complicated shapes tin can be performed by making plastic models of them and observing them through crossed filters, as seen in (Figure). It is apparent that the upshot depends on wavelength as well as stress. The wavelength dependence is sometimes also used for artistic purposes.

Optical stress analysis of a plastic lens placed betwixt crossed polarizers. (credit: "Infopro"/Wikimedia Eatables)

The figure shows a photograph of a plastic lens that is being squeezed by a clamp. Rainbow patterns appear, showing the deformation of the lens. The colored regions are outlined by dark curves connecting the centers of the edges of the lens.

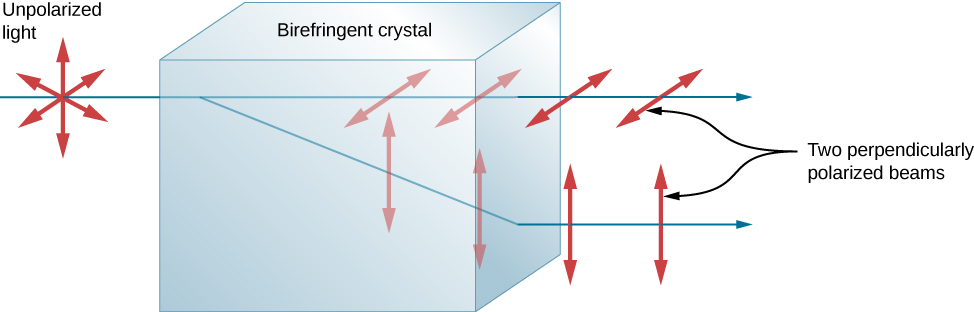
Another interesting phenomenon associated with polarized calorie-free is the ability of some crystals to split up an unpolarized beam of light into two polarized beams. This occurs because the crystal has one value for the index of refraction of polarized calorie-free but a different value for the index of refraction of light polarized in the perpendicular direction, then that each component has its ain angle of refraction. Such crystals are said to be birefringent, and, when aligned properly, ii perpendicularly polarized beams will emerge from the crystal ((Figure)). Birefringent crystals tin can be used to produce polarized beams from unpolarized light. Some birefringent materials preferentially blot i of the polarizations. These materials are chosen dichroic and can produce polarization past this preferential absorption. This is fundamentally how polarizing filters and other polarizers work.

Birefringent materials, such as the common mineral calcite, split up unpolarized beams of light into two with two dissimilar values of index of refraction.

$The figure shows a horizontal, unpolarized ray of light incident on a block labeled birefringent crystal. The ray is perpendicular to the face of the crystal where it enters it. The incident ray splits into two rays when it enters the crystal. One part of the ray continues straight on. This ray is horizontally polarized. The other part of the ray propagates at an. This ray is vertically polarized. The second ray refracts upon leaving the crystal such that the two rays are parallel outside the crystal. The rays are labeled as two perpendicularly polarized beams.$

Summary

Conceptual Questions

Tin can a sound wave in air be polarized? Explain.

No. Audio waves are not transverse waves.

No light passes through ii perfect polarizing filters with perpendicular axes. However, if a third polarizing filter is placed betwixt the original two, some low-cal tin pass. Why is this? Under what circumstances does near of the light pass?

Explain what happens to the energy carried by light that information technology is dimmed by passing information technology through two crossed polarizing filters.

Energy is absorbed into the filters.

Using the information given in the preceding question, explicate why sunsets are ruddy.

Sunsets are viewed with light traveling straight from the Sun toward us. When bluish low-cal is scattered out of this path, the remaining ruby-red light dominates the overall advent of the setting Sun.

When low-cal is reflected at Brewster's angle from a shine surface, it is $100\text{%}$ polarized parallel to the surface. Part of the light will be refracted into the surface. Describe how you would practise an experiment to determine the polarization of the refracted light. What management would you expect the polarization to take and would you expect it to be $100\text{%}$ ?

If y'all lie on a beach looking at the water with your head tipped slightly sideways, your polarized sunglasses do non piece of work very well. Why not?

The axis of polarization for the sunglasses has been rotated $90\text{°}$ .

Problems

What angle is needed between the direction of polarized calorie-free and the axis of a polarizing filter to cut its intensity in half?

The angle between the axes of ii polarizing filters is $45.0\text{°}$ . By how much does the second filter reduce the intensity of the low-cal coming through the first?

0.500

Suppose that in the preceding problem the light incident on ${\text{P}}_{1}$ is unpolarized. At the adamant value of $\theta$ , what fraction of the incident calorie-free passes through the combination?

0.125 or 1/eight

If you lot take completely polarized light of intensity $150\phantom{\rule{0.2em}{0ex}}{\text{W/m}}^{2}$ , what will its intensity be after passing through a polarizing filter with its axis at an $89.0\text{°}$ bending to the light'south polarization direction?

What angle would the centrality of a polarizing filter need to make with the direction of polarized light of intensity $1.00\phantom{\rule{0.2em}{0ex}}{\text{kW/m}}^{2}$ to reduce the intensity to $10.0\phantom{\rule{0.2em}{0ex}}{\text{W/m}}^{2}$ ?

$84.3\text{°}$

At the terminate of (Effigy), it was stated that the intensity of polarized light is reduced to $90.0\text{%}$ of its original value past passing through a polarizing filter with its centrality at an bending of $18.4\text{°}$ to the direction of polarization. Verify this statement.

Show that if you lot have three polarizing filters, with the 2d at an angle of $45.0\text{°}$ to the get-go and the third at an angle of $90.0\text{°}$ to the first, the intensity of light passed by the first will be reduced to $25.0\text{%}$ of its value. (This is in dissimilarity to having only the first and third, which reduces the intensity to cypher, and so that placing the second between them increases the intensity of the transmitted calorie-free.)

$0.250\phantom{\rule{0.2em}{0ex}}{I}_{0}$

Iii polarizing sheets are placed together such that the transmission axis of the 2d sheet is oriented at $25.0\text{°}$ to the axis of the first, whereas the transmission axis of the third sheet is oriented at $40.0\text{°}$ (in the same sense) to the axis of the first. What fraction of the intensity of an incident unpolarized axle is transmitted by the combination?

It is institute that when light traveling in water falls on a plastic block, Brewster'south angle is $50.0\text{°}$ . What is the refractive index of the plastic?

At what bending volition light reflected from diamond exist completely polarized?

$67.54\text{°}$

What is Brewster's angle for low-cal traveling in h2o that is reflected from crown glass?

A scuba diver sees calorie-free reflected from the water's surface. At what angle relative to the water'south surface volition this light exist completely polarized?

$53.1\text{°}$

Boosted Problems

From his measurements, Roemer estimated that it took 22 min for calorie-free to travel a distance equal to the diameter of Earth'south orbit around the Sun. (a) Use this estimate along with the known diameter of Earth'due south orbit to obtain a crude value of the speed of low-cal. (b) Light really takes sixteen.5 min to travel this distance. Use this time to calculate the speed of calorie-free.

Cornu performed Fizeau'due south measurement of the speed of low-cal using a wheel of diameter 4.00 cm that independent 180 teeth. The distance from the wheel to the mirror was 22.9 km. Assuming he measured the speed of low-cal accurately, what was the angular velocity of the wheel?

114 radian/due south

Suppose y'all take an unknown articulate substance immersed in water, and yous wish to identify it by finding its alphabetize of refraction. You arrange to accept a axle of light enter it at an bending of $45.0\text{°}$ , and you notice the angle of refraction to exist $40.3\text{°}$ . What is the index of refraction of the substance and its likely identity?

Shown below is a ray of light going from air through crown glass into h2o, such as going into a fish tank. Calculate the amount the ray is displaced by the drinking glass $\left(\text{Δ}x\right),$ given that the incident angle is $40.0\text{°}$ and the drinking glass is 1.00 cm thick.

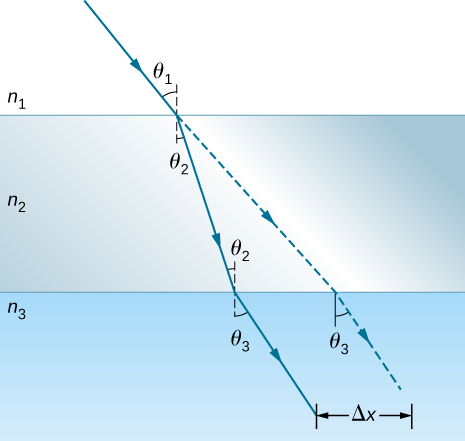
$The figure illustrates refraction occurring when light travels from medium n 1 to n 3 through an intermediate medium n 2. The incident ray makes an angle theta 1 with a perpendicular drawn at the point of incidence at the interface between n 1 and n 2. The light ray entering n 2 bends towards the perpendicular line making an angle theta 2 with it on the n 2 side. The ray arrives at the interface between n 2 and n 3 at an angle of theta 2 to a perpendicular drawn at the point of incidence at this interface, and the transmitted ray bends away from the perpendicular, making an angle of theta three to the perpendicular on the n 3 side. A straight line extrapolation of the original incident ray is shown as a dotted line. This line is parallel to the refracted ray in the third medium, n 3, and is shifted a distance delta x from the refracted ray. The extrapolated ray is at the same angle theta three to the perpendicular in medium n 3 as the refracted ray.$

three.72 mm

Considering the previous problem, show that ${\theta }_{3}$ is the same as it would be if the second medium were not present.

At what angle is lite within crown glass completely polarized when reflected from water, as in a fish tank?

$41.2\text{°}$

Calorie-free reflected at $55.6\text{°}$ from a window is completely polarized. What is the window's index of refraction and the probable substance of which it is made?

(a) Calorie-free reflected at $62.5\text{°}$ from a gemstone in a ring is completely polarized. Can the gem be a diamond? (b) At what angle would the light be completely polarized if the gem was in water?

a. 1.92. The gem is not a diamond (it is zircon). b. $55.2\text{°}$

Unreasonable results Suppose light travels from water to some other substance, with an angle of incidence of $10.0\text{°}$ and an angle of refraction of $14.9\text{°}$ . (a) What is the alphabetize of refraction of the other substance? (b) What is unreasonable almost this upshot? (c) Which assumptions are unreasonable or inconsistent?

a. 0.898; b. We cannot have $n<1.00$ , since this would imply a speed greater than c. c. The refracted bending is likewise large relative to the angle of incidence.

Unreasonable results Light traveling from h2o to a gemstone strikes the surface at an bending of $80.0\text{°}$ and has an angle of refraction of $15.2\text{°}$ . (a) What is the speed of light in the gemstone? (b) What is unreasonable well-nigh this result? (c) Which assumptions are unreasonable or inconsistent?

If a polarizing filter reduces the intensity of polarized light to

*** QuickLaTeX cannot compile formula: l.0\text{%}  *** Error bulletin: File ended while scanning use of \text@. Emergency terminate.

of its original value, past how much are the electric and magnetic fields reduced?

$0.707\phantom{\rule{0.2em}{0ex}}{B}_{1}$

Suppose yous put on two pairs of polarizing sunglasses with their axes at an bending of $15.0\text{°}$ . How much longer will it accept the light to deposit a given amount of energy in your eye compared with a single pair of sunglasses? Assume the lenses are clear except for their polarizing characteristics.

(a) On a day when the intensity of sunlight is $1.00\phantom{\rule{0.2em}{0ex}}{\text{kW/m}}^{2}$ , a round lens 0.200 m in bore focuses light onto water in a blackness beaker. Two polarizing sheets of plastic are placed in front of the lens with their axes at an angle of $20.0\text{°}$ . Assuming the sunlight is unpolarized and the polarizers are $100\text{%}$ efficient, what is the initial charge per unit of heating of the h2o in $\text{°}\text{C/s}$ , assuming it is

*** QuickLaTeX cannot compile formula: eighty.0\text{%}  *** Mistake bulletin: File concluded while scanning apply of \text@. Emergency stop.

absorbed? The aluminum beaker has a mass of 30.0 grams and contains 250 grams of water. (b) Do the polarizing filters get hot? Explain.

a. $1.69\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-2}\text{°}\text{C/s}$ ; b. yeah

Challenge Problems

Light shows staged with lasers utilise moving mirrors to swing beams and create colorful furnishings. Testify that a light ray reflected from a mirror changes management by $2\theta$ when the mirror is rotated by an angle $\theta$ .

Consider sunlight inbound Earth'due south temper at sunrise and sunset—that is, at a $90.0\text{°}$ incident angle. Taking the boundary betwixt nearly empty space and the atmosphere to be sudden, calculate the angle of refraction for sunlight. This lengthens the fourth dimension the Lord's day appears to be higher up the horizon, both at sunrise and dusk. Now construct a trouble in which you lot decide the angle of refraction for dissimilar models of the atmosphere, such equally various layers of varying density. Your teacher may wish to guide you on the level of complexity to consider and on how the index of refraction varies with air density.

First part: $88.6\text{°}$ . The remainder depends on the complexity of the solution the reader constructs.

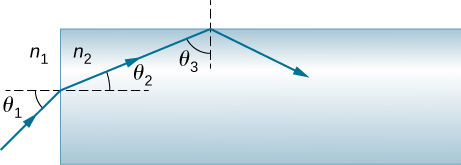
A low-cal ray entering an optical fiber surrounded by air is get-go refracted and and then reflected as shown beneath. Prove that if the fiber is made from crown drinking glass, any incident ray will be totally internally reflected.

$The figure shows light traveling from n 1 and incident onto the left face of a rectangular block of material n 2. The ray is incident at an angle of incidence theta 1, measured relative to the normal to the surface where the ray enters. The angle of refraction is theta 2, again, relative to the normal to the surface. The refracted ray falls onto the upper face of the block and gets totally internally reflected with theta 3 as the angle of incidence.$

A calorie-free ray falls on the left confront of a prism (come across below) at the bending of incidence $\theta$ for which the emerging beam has an angle of refraction $\theta$ at the right face up. Bear witness that the alphabetize of refraction north of the glass prism is given past

$n=\frac{\text{sin}\phantom{\rule{0.2em}{0ex}}\frac{1}{2}\left(\alpha +\varphi \right)}{\text{sin}\phantom{\rule{0.2em}{0ex}}\frac{1}{2}\varphi }$

where $\varphi$ is the vertex angle of the prism and $\alpha$ is the angle through which the axle has been deviated. If $\alpha =37.0\text{°}$ and the base of operations angles of the prism are each $50.0\text{°},$ what is northward?

$A light ray falls on the left face of a triangular prism whose upper vertex has an angle of phi and whose index of refraction is n. The angle of incidence of the ray relative to the normal to the left face is theta. The ray refracts in the prism. The refracted ray is horizontal, parallel to the base of the prism. The refracted ray reaches the right face of the prism and refracts as it emerges out of the prism. The emerging ray makes an angle of theta with the normal to the right face.$